그래프 알고리즘, 깊이/너비 우선 탐색(DFS/BFS)

그래프란?

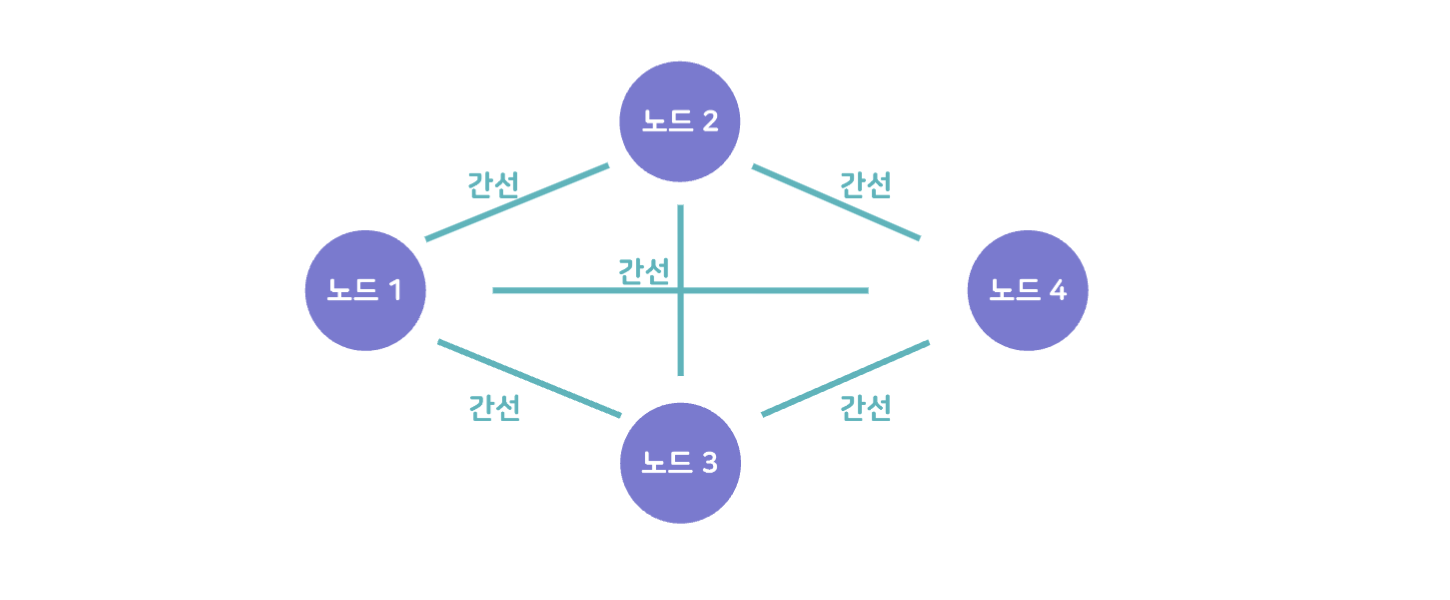
정점과 간선으로 이루어진 자료구조로 정점간의 관계를 조직도로 표현한다.

 

🔎 정점: 여러가지 특성을 가질 수 있는 객체

🔎 간선: 정점들 간의 관계

 

 

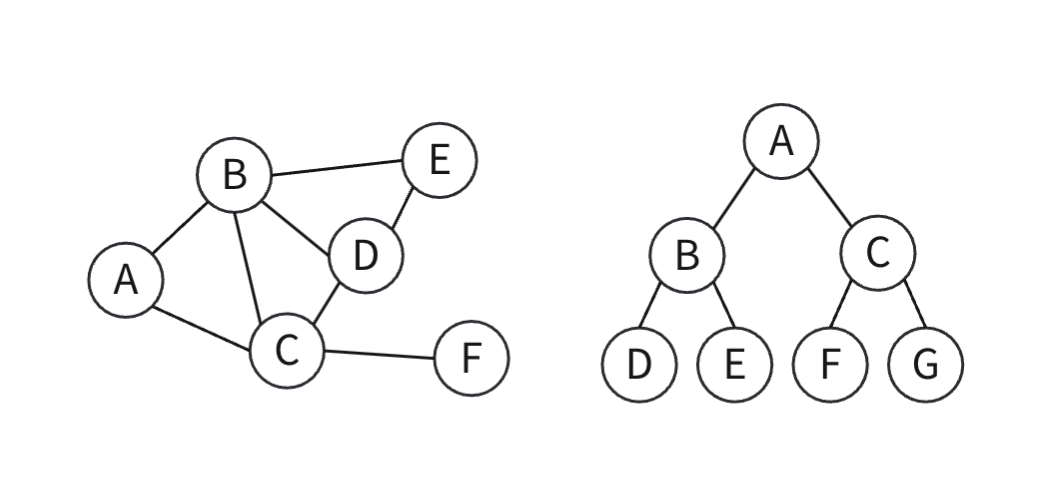
그래프의 종류

무방향 그래프: 정점간 간선에 방향이 없는 그래프

 

 

 

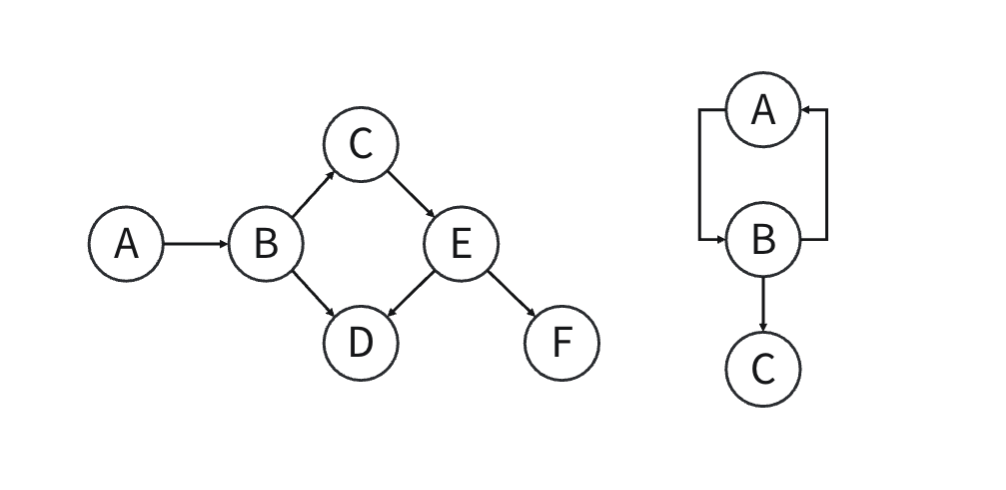
방향 그래프: 정점간 간선에 방향이 있는 그래프

 

 

그래프 알고리즘

너비우선탐색(BFS, Breadth-First Search): 탐색을 시작하는 노드로부터 거리순으로 방문하는 탐색 알고리즘

 

큐(Queue)로 구현하기

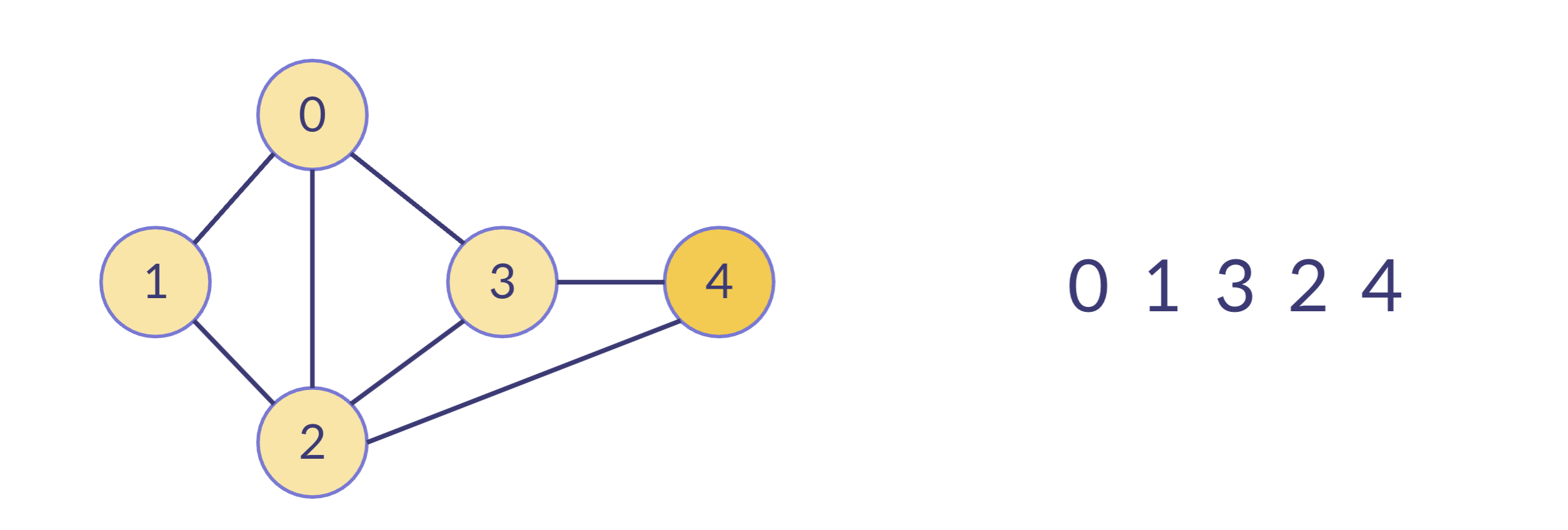
function bfs(graph, root) {
    const visited = new Set([root]); // 중복 방문 방지
    const result = []; // 탐색 결과 저장
    const queue = [root]; // 시작 노드로 큐 설정

    // 큐가 비어있지 않을 때 실행
    while (queue.length > 0) {
        const cur = queue.shift();
        result.push(cur);

        // 현재 노드의 인접 노드를 확인하면서 방문하지 않은 노드는 큐와 visited에 추가
        for (const node of graph[cur]) {
            if (!visited.has(node)) {
                queue.push(node);
                visited.add(node);
            }
        }
    }

    return result;
}

시작 노드(0)를 큐에 추가하고 해당 노드를 방문처리 하기 위해서 shift 하기

현재 노드와 연결된 노드 중 방문하지 않은 노드를 큐에 추가하고 추가한 shift 해서 노드를 방문처리하는 과정 반복

 

 

 

깊이우선탐색(DFS, Depth-First Search): 시작하는 노드로부터 갈 수 있는 깊은곳까지 탐색하기를 반복하는 알고리즘

 

스택(Stack)으로 구현하기

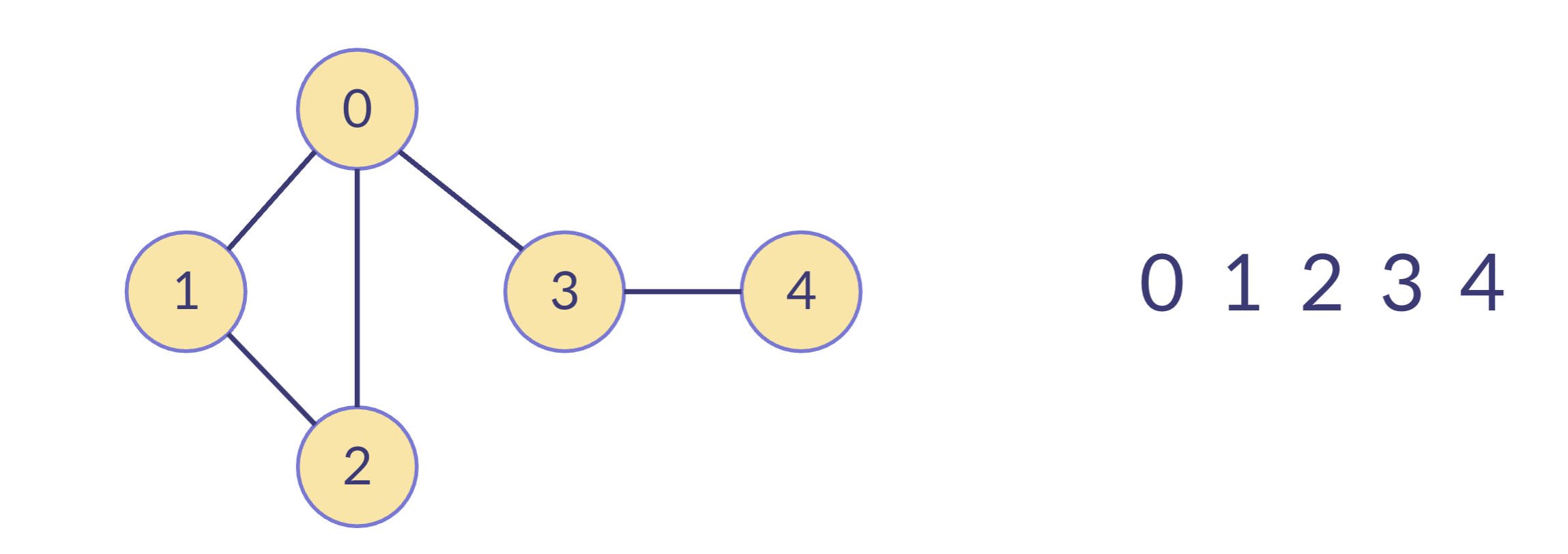
function dfs(graph, start) {
    const result = []; // 방문한 노드 저장
    const visited = new Set(); // 방문한 노드 중복 방문 방지
    const stack = [start]; // 시작 노드 초기화

    // 스택이 비어있지 않으면 실행
    while (stack.length > 0) {
        const node = stack.pop();

        // 방문하지 않은 노드만 실행
        if (!visited.has(node)) {
            visited.add(node);
            result.push(node);
            stack.push(...graph[node]);
        }
    }

    return result;
}

시작노드(0)부터 방문해서 방문한 노드를 스택에 추가하고 0을 pop해서 방문처리

0과 연결된 노드 중 방문하지 않은 노드를 스택에 넣고  pop해서 방문 처리 하는 과정 반복

스택이 빌 때까지 반복하고 스택에 더 이상 꺼낼 노드가 없다면 탐색 종료 

 

 

Reference 엘리스