-
728x90
동적계획법(Dynamic Programming, DP) 이란?
복잡한 문제를 간단한 여러 개의 하위 문제로 나누어 푸는 방법
동적계획법은 재귀적인 방법이지만, 중복 계산을 피하기 위해서 메모이제이션(Memoization) 또는 반복적인 방법을 사용하여 구한다.
메모이제이션은 계산한 값을 저장해두고 필요할 때 불러와서 중복계산을 피하는 방식
동적계획법 문제의 특성
- 중복되는 부분 문제(Overlapping Subproblem): 작은 하위 문제들이 중복되어 나타난다.
- 최적 부분 구조(Optimal Substructure): 전체 문제의 최적해결 방법을 부분 문제의 최적해결 방법으로 구할 수 있다.
피보나치 수열
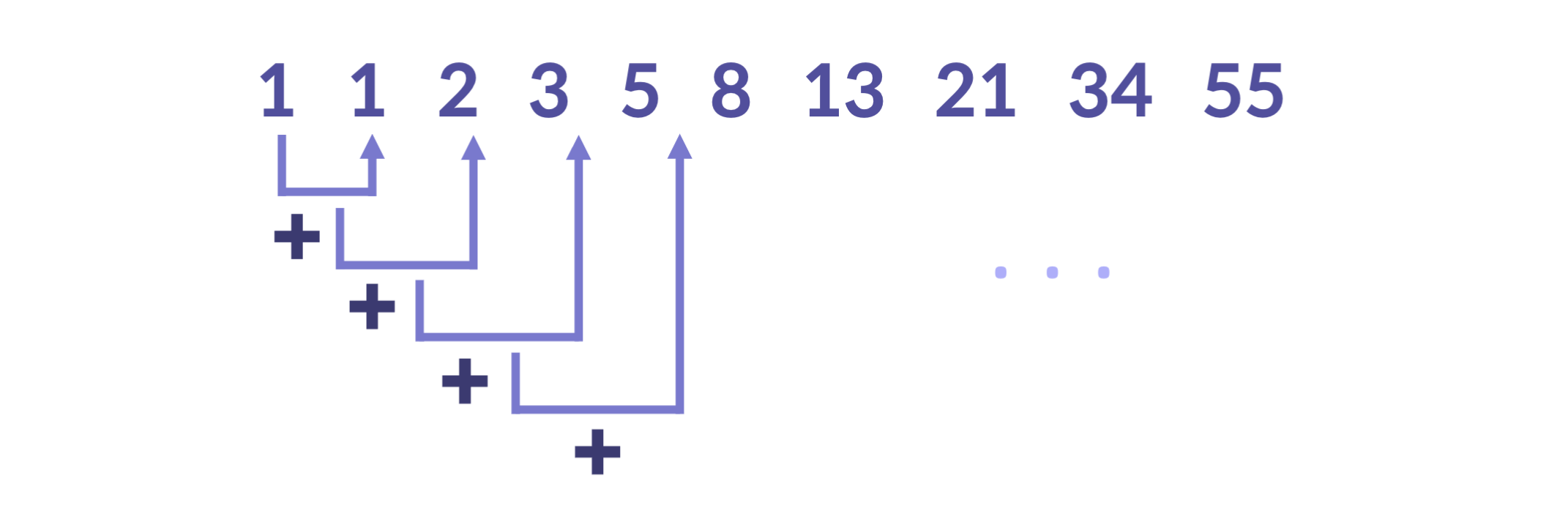
피보나치 수열이란? 이전 두 항의 합이 다음 항이 되는 수열을 말한다.
재귀를 통한 피보나치 수열
function fibo(n) { if (n < 3) { return 1; } else { return fibo(n - 1) + fibo(n - 2); } }만약 n이 3보다 작으면 1을 반환(피보나치 수열은 첫 번째, 두 번째 항이 모두 1이기 때문에)
그렇지 않으면 fibo(n-1) + fibo(n-2) 합으로 재귀적으로 호출한다.

하지만, 이 방식은 왼쪽에서 이미 계산한 f(3)을 오른쪽에서 또 계산하기 때문에 중복 계산되어 비효율적이게 된다.
이러한 문제를 동적계획법을 사용해서 해결할 수 있다.
동적계획법을 구현하는 테크닉
점화식: 복잡한 문제를 작은 하위 문제로 표현한 식
ex) f(n) = f(n - 1) + f(n - 2)
- 구하고자 하는 값이 무엇인지 정의 => f(n): n번째 피보나치 수열
- 구하고자 하는 값을 부분문제들로 표현, 피보나치 수열의 n번째 항은 n - 1항과 n - 2항의 합이다.
Top-down (재귀호출 방식)
- 큰 문제를 작은 문제로 나눈다.
- 작은 문제를 풀어 return 해준다.
function fiboTopDown(n, memo) { // memo 객체가 없을 경우 초기화 memo = memo || {}; // n이 0또는 1일 경우 1 반환(첫 번째, 두 번째 항은 1) if (n <= 1) { return 1; } // 이미 계산한 값이 있는지 확인 if (!memo[n]) { memo[n] = fiboTopDown(n - 1, memo) + fiboTopDown(n - 2, memo); } return memo[n]; // 저장된 값 반환 }함수 내부에 memo라는 객체를 활용해서 이미 계산된 값을 저장하고 중복 계산을 피하는 코드로써,
함수를 호출 할 때 fiboTopDown(4, {}) 이런식으로 memo를 생략하면 자동으로 빈 객체로 초기화되도록 한다.
Bottom-down (반복문 방식)
- 작은 문제부터 차례로 풀어 적는다.
- 크기를 조금씩 늘려서 문제를 푼다.
function fiboBottomUp(n) { const dp = []; // 첫 번째, 두 번째 항 설정 dp[0] = 0; dp[1] = 1; for (let i = 2; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; // n번째 피보나치 수열 값 반환 }반복문을 통해 dp[i]에 dp[i - 1]과 dp[i - 2]의 합이 저장되어 현재 항(i)의 피보나치 수열 값이 된다.
이렇게 작은 문제부터 차례로 해결해서 최종적으로 n번째 피보나치 수열 값을 얻을 수 있다.
Reference 엘리스
'코딩테스트, 알고리즘' 카테고리의 다른 글
연속 부분 최대합으로 알아보는 완전탐색과 시간복잡도 (1) 2023.11.26 동전 거스름돈으로 알아보는 탐욕 알고리즘 (Greedy Algorithm) (0) 2023.11.17 [백준] 9095번 1, 2, 3 더하기 (0) 2023.11.06 [백준] 1436번 영화감독 숌 (node.js) (0) 2023.10.23 [백준] 1316번 그룹 단어 체커 (node.js) (0) 2023.10.22 댓글
Written by Jieun
👩🏻💻 내 마음대로 Today I Learned
